1. Bounded inverse theorem (a bijective bounded linear operator T from one Banach space to another has bounded inverse )
2. Hahn-Banach theorem (to extend bounded linear functions on a subspace/v.s. to the whole space)
3. Hellinger-Toeplitz theorem (...symmetric operator on a Hilbert space is bounded)
4. Riesz representation theorem (to map Hilbert space H towards its dual space H*)
Fréchet-Riesz theorem: Φ: H → H* defined by Φ(x) = φx is an isometric (anti-) isomorphism. Quantum Mechanics: every ket
 has a corresponding bra
has a corresponding bra  ,
,5. Banach-Steinhaus theorem (Uniform boundedness principle)
For continuous linear operators whose domain is a Banach space, pointwise boundedness is
equivalent to uniform boundedness in operator norm.
=================================================================
Top 5 Theorems in Real Analysis and Measure Theory
1. Bolzano–Weierstrass theorem (each bounded sequence in R^n has a convergent subsequence)
2. Fatou–Lebesgue theorem (a chain of inequalities relating Lebesgue integrals)
Dominated convergence theorem (a special case of Fatou–Lebesgue theorem.)
3. Fundamental theorem of calculus, Mean value theorem, Taylor's theorem (for Engineers like me):
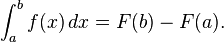


4. Heine–Borel theorem (A subset of a metric space is compact iff it is complete and totally bounded)
5. Uniform limit theorem (the uniform limit of any sequence of continuous functions is continuous.)
==================================================================
Top 5 Inequalities in Real Analysis (with minimum words:)
1. Hölder's inequality:
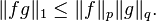
(A special case) Cauchy–Schwarz inequality:
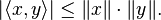
2. Minkowski inequality:

(A special case) Triangle inequality:

3. Chebyshev's inequality:

4. Inequality of arithmetic and geometric means:
![\frac{x_1+x_2+\cdots+x_n}{n} \ge \sqrt[n]{x_1x_2 \cdots x_n}](http://upload.wikimedia.org/math/5/9/2/59233828a7dfbc48a6432c0e05a91d32.png)
5. Jensen's inequality:


No comments:
Post a Comment