Another similar question is "how can I sort a 10G of data while I have only 4G of memory"?
The answer should be "correlated" to "External Sorting" and "Internal Sorting", and usually beyond the in-memory sorting taught in general algorithm textbook.
Here are the links to two articles:
"Implementing Sorting in Database Systems" by GOETZ GRAEFE from Microsoft provides more detailed discussion on the sorting algorithm in DBMS.
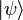 has a corresponding bra
has a corresponding bra  ,
,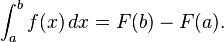


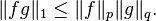
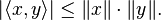



![\frac{x_1+x_2+\cdots+x_n}{n} \ge \sqrt[n]{x_1x_2 \cdots x_n}](http://upload.wikimedia.org/math/5/9/2/59233828a7dfbc48a6432c0e05a91d32.png)

